Assalamu'alaikum Wr. Wb. Pada postingan ini saya akan membagikan cara memprediksi penyebaran kasus COVID-19 di Indonesia menggunakan Logistic Sigmoid Function dengan Bahasa Pemrograman Python pada Google Colab. Metode ini dilakukan dengan cara memetakan (fitting) kurva jumlah kasus penyebaran ke dalam fungsi logistik sigmoid sehingga dapat diperoleh hasil prediksi dari kurva sigmoid yang parameternya dimasukkan ke persamaan Logistic Function. Persamaan yang digunakan dalam perhitungan dengan metode tersebut yaitu:
Bentuk kurva dari fungsi sigmoid dapat dilihat pada gambar di bawah.
Namun pada postingan ini tidak akan dijelaskan secara rinci bagaimana cara perhitungannya. Jika Anda ingin mengetahuinya dapat mengunjungi link berikut.
- https://en.wikipedia.org/wiki/Logistic_function
- https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/build-a-logistic-model-from-data/
Sedangkan untuk persamaan dan parameter yang digunakan sebagai pemodelan pada program ini dapat dilihat pada link berikut.
Langkah-langkah yang harus dilakukan adalah:
- Unduh dataset penyebaran COVID-19 per hari (format *.csv) di Indonesia di sini:
- Buka file-nya pada Ms. Excel kemudian hapus baris kedua kemudian Save untuk mempermudah dalam pemrograman sehingga tidak perlu dihapus pada DataFrame-nya.


- Setelah disimpan, upload dataset tersebut ke Github. Jika tidak memiliki akun Github Anda dapat menyimpan dataset tersebut pada direktori penyimpanan sementara yang disediakan oleh Google Colab. Caranya cukup mudah dan hanya mengubah sedikit kode seperti pada gambar berikut.

- Selanjutnya buka Google Colab dan masukkan sourcecode untuk import library yang dibutuhkan di bawah ini.
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- import plotly.express as px
- from scipy.optimize import curve_fit
- from datetime import datetime, timedelta
- Untuk mengambil dataset yang telah di-upload ke Github, tambahkan kode berikut.
- !apt-get install subversion > /dev/null
- !svn export https://github.com/Vidi005/COVID-19-Prediction-Indonesia/trunk/datasets > /dev/null
- Selanjutnya ubah nama header tabel dan tampilkan tabelnya untuk mempermudah dalam pengecekan.
- data=pd.read_csv("datasets/Daily-Update IDN-COVID19 - Sheet5.csv")
- data=data.rename(columns={"Date": "Tanggal",
- "New_case_per_day": "Terkonfirmasi",
- "Death_cases_perDay": "Meninggal",
- "Recovered-cases_perDay": "Sembuh",
- "Treatment_cases_perDay": "Aktif",
- "Recovered_cases": "Jumlah Sembuh",
- "Total_death": "Jumlah Meninggal",
- "Patient_under_treatment": "Jumlah Aktif",
- "Cumulative_cases": "Jumlah Kasus"})
- data.head(-1)
- Tampilkan juga visualisasi data kasus per harinya dalam bentuk grafik garis agar mudah dilihat perkembangannya.
- fig = plt.figure(figsize=(7, 4))
- fig.set_figheight(10)
- fig.set_figwidth(15)
- plt.subplot(2, 2, 1)
- plt.plot(data.aggregate("Terkonfirmasi",axis=0), marker="o", color="orange")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Terinfeksi")
- plt.title("Terkonfirmasi per-hari", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 2)
- plt.plot(data.aggregate("Meninggal",axis=0), marker="o", color="black")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Meninggal")
- plt.title("Kematian per-hari", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 3)
- plt.plot(data.aggregate("Sembuh",axis=0), marker='o')
- plt.xlabel("Hari ke-n")
- plt.ylabel("Pasien Sembuh")
- plt.title("Sembuh per-hari", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 4)
- plt.plot(data.aggregate("Aktif",axis=0), marker='o', color="purple")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Pasien Aktif")
- plt.title("Dalam Pengobatan per-hari", size=15)
- plt.grid(zorder = 0)
- plt.show()
- Hasil output-nya akan seperti ini.

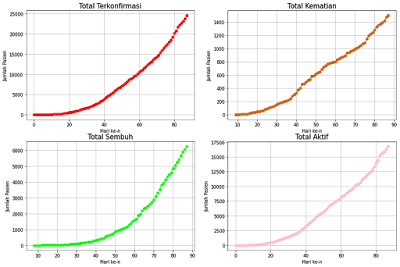
- Tampilkan juga grafik perkembangan dari jumlah kasusnya.
- fig = plt.figure(figsize = (10, 7))
- fig.set_figheight(10)
- fig.set_figwidth(15)
- plt.subplot(2, 2, 1)
- plt.plot(data.aggregate("Jumlah Kasus",axis=0), marker="o", color="red")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Jumlah Pasien")
- plt.title("Total Terkonfirmasi", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 2)
- plt.plot(data.aggregate("Jumlah Meninggal",axis=0), marker="o", color="chocolate")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Jumlah Pasien")
- plt.title("Total Kematian", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 3)
- plt.plot(data.aggregate("Jumlah Sembuh",axis=0), marker="o", color="lime")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Jumlah Pasien")
- plt.title("Total Sembuh", size=15)
- plt.grid(zorder = 0)
- plt.subplot(2, 2, 4)
- plt.plot(data.aggregate("Jumlah Aktif",axis=0), marker="o", color="pink")
- plt.xlabel("Hari ke-n")
- plt.ylabel("Jumlah Pasien")
- plt.title("Total Aktif", size=15)
- plt.grid(zorder = 0)
- plt.show()
- Setelah program dijalankan output-nya akan seperti ini.
- Kemudian buat fungsi kurva fungsi logistik untuk memetakan grafik penyebaran jumlah kasusnya pada fungsi sigmoid.
- def plot_predict(case, future_days):
- def avg_err(pcov):
- return np.round(np.sqrt(np.diag(pcov)).mean(), 2)
- # function to be minimized
- def f_sigmoid(x, a, b, c):
- # a = sigmoid midpoint
- # b = curve steepness (logistic growth)
- # c = max value
- return (c / (1 + np.exp(-b*(x-a))))
- inception = 0
- graph = data.groupby("Tanggal")[["Jumlah Kasus", "Jumlah Meninggal", "Jumlah Sembuh"]].sum().reset_index()[inception:]
- y = graph[case]
- x = np.arange(len(y))
- # fitting the data on the logistic function
- popt_sig, pcov_sig = curve_fit(f_sigmoid, x, y, method="dogbox", bounds=([12., 0.001, y.mean()],[120., 2.5, 10*y.max()]))
- print(popt_sig)
- peakday = datetime.strftime(datetime.strptime(graph["Tanggal"][inception], "%Y-%m-%d")+timedelta(days=int(popt_sig[0])), "%Y-%m-%d")
- plt.figure(figsize=(14,7))
- x_m = np.arange(len(y)+future_days)
- y_m = f_sigmoid(x_m, *popt_sig)
- print("Prediksi:")
- for i in range(1,90):
- pday = datetime.strftime(datetime.strptime(graph["Tanggal"][inception], "%Y-%m-%d")+timedelta(days=len(y)+i-1), "%Y-%m-%d")
- print("%s: %d" % (pday, y_m[len(y)+i-1]))
- plt.plot(x[-1]+i, y_m[len(y)+i-1], marker="o", c="g")
- plt.plot(x, y, c="g", marker="o", label="Prediksi")
- # creating the matplotlib visualization
- plt.plot(x_m, y_m, c="gray", marker="x", label="Sigmoid | error: "+str(avg_err(pcov_sig)))
- plt.text(x_m[-1]+.5, y_m[-1], str(int(y_m[-1])), size = 10)
- plt.plot(x, y, c="r", marker="o", label = case)
- plt.xlabel("Hari ke- ")
- plt.ylabel("Jumlah Terinfeksi")
- plt.legend(prop={"size": 15})
- plt.title("Prediksi Penyebaran COVID-19 Indonesia", size=15)
- plt.axvline(x[-1])
- plt.text(x[-1]-.5, y_m[-1], str(graph["Tanggal"][len(y)+inception-1]), size = 10)
- plt.axvline(int(popt_sig[0]))
- plt.text(int(popt_sig[0]), 1, "Puncak: Hari ke - " + str(int(popt_sig[0])) + " (" + peakday + ")", size = 10)
- plt.grid(zorder = 0)
- plt.show()
- Setelah itu tambahkan kode berikut untuk menampilkan hasil prediksinya.
- plot_predict("Jumlah Kasus", 90)
- Output-nya akan seperti ini.

Dapat dilihat dari hasil prediksi tersebut bahwa terdapat error yang cukup besar, hal itu disebabkan masih fluktuatifnya kurva dari jumlah kasus terkonfirmasi per harinya sehingga masih sulit untuk diprediksi. Hasil prediksi dengan metode ini akan semakin akurat jika kurva perkembangan kasusnya sudah mulai menurun dan tidak terjadi lagi peningkatan jumlah kasus per harinya. Sehingga perlunya pembaruan dataset kembali jika kurvanya masih fluktuatif. Untuk puncak kasus tersebut merupakan nilai tengah dari hari ke-n.
Program tersebut diatur untuk memprediksi sampai 90 hari ke depan, Anda dapat mengubahnya sesuai keinginan dengan syarat prediksi jumlah kasus tidak boleh melebihi kurva fungsi sigmoid yang ditentukan.
Angka 120 pada fungsi tersebut yang ditandai digunakan untuk panjang rentang kurva sigmoid.
Sedangkan angka 90 digunakan untuk menampilkan hasil prediksi selama 90 hari. Hasil prediksi pertama diperoleh lebih rendah dari kasus sebelumnya dikarenakan adanya error pada sigmoid sebesar 505,88. Hal itu disebabkan hasil prediksi hanya mengikuti bentuk dari kurva sigmoid yang di-fit-kan ke dalam kurva penyebaran kasusnya. - Buat fungsi baru pada baris kode baru untuk menampilkan hasil per harinya.
- def plot_predict(case, future_days):
- def avg_err(pcov):
- return np.round(np.sqrt(np.diag(pcov)).mean(), 2)
- # function to be minimized
- def f_sigmoid(x, a, b, c):
- # a = sigmoid midpoint
- # b = curve steepness (logistic growth)
- # c = max value
- return (c / (1 + np.exp(-b*(x-a))))
- day = 0
- graph_day = data.groupby("Tanggal")[["Jumlah Kasus", "Meninggal", "Sembuh"]].sum().reset_index()[day:]
- y = graph_day[case]
- x = np.arange(len(y))
- popt_sig, pcov_sig = curve_fit(f_sigmoid, x, y, method="dogbox", bounds=([12., 0.001, y.mean()],[120., 2.5, 10*y.max()]))
- print(popt_sig)
- peakday = datetime.strftime(datetime.strptime(graph_day["Tanggal"][day], "%Y-%m-%d")+timedelta(days=int(popt_sig[0])), "%Y-%m-%d")
- plt.figure(figsize=(14,7))
- x_m = np.arange(len(y)+future_days)
- y_m = f_sigmoid(x_m, *popt_sig)
- for i in range(1,90):
- pday = datetime.strftime(datetime.strptime(graph_day["Tanggal"][day], "%Y-%m-%d")+timedelta(days=len(y)+i-1), "%Y-%m-%d")
- plt.plot(x[-1]+i, (y_m[len(y)+i])-(y_m[len(y)+i-1]), marker="o", c="g")
- #plt.plot(x_m, (y_m-y_m[i-1]), c="gray", marker="x")
- plt.plot(data.aggregate("Terkonfirmasi",axis=0), marker="o", color="orange", label="Kasus per hari")
- plt.axvline(x[-1])
- plt.text(x[-1]-.5, y_m[0], str(graph_day["Tanggal"][len(y)+day-1]), size = 10)
- plt.axvline(int(popt_sig[0]))
- plt.text(int(popt_sig[0]), 1, "Puncak: Hari ke - " + str(int(popt_sig[0])) + " (" + peakday + ")", size = 10)
- plt.xlabel("Hari ke-n")
- plt.ylabel("Terinfeksi")
- plt.title("Prediksi Penyebaran per-hari", size=15)
- plt.plot(x[-1]+i, (y_m[len(y)+i])-(y_m[len(y)+i-1]), c="g", marker="o", label="Prediksi")
- plt.legend(prop={"size": 15})
- plt.grid(zorder=0)
- plt.show
- Terakhir, tampilkan hasil prediksinya.
- plot_predict("Jumlah Kasus", 90)
- Hasilnya seperti di bawah ini.

Dataset yang digunakan pada postingan ini menggunakan dataset telah yang diperbaharui pada 28 Mei 2020. Untuk memperbarui dataset-nya dapat dilakukan kembali langkah 1-3 dan jalankan kembali programnya.


